# prepare datasets
X = df[['Petal length', 'Petal width']].values[30:150,]
y, y_label = pd.factorize(df['Class label'].values[30:150])
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.33, random_state=1)
print('#Training data points: %d + %d + %d = %d' % ((y_train == 0).sum(),
(y_train == 1).sum(),
(y_train == 2).sum(),
y_train.size))
print('#Testing data points: %d + %d + %d = %d' % ((y_test == 0).sum(),
(y_test == 1).sum(),
(y_test == 2).sum(),
y_test.size))
print('Class labels: %s (mapped from %s)' % (np.unique(y), np.unique(y_label)))
# standarize X
sc = StandardScaler()
sc.fit(X_train)
X_train_std = sc.transform(X_train)
X_test_std = sc.transform(X_test)
# training & testing
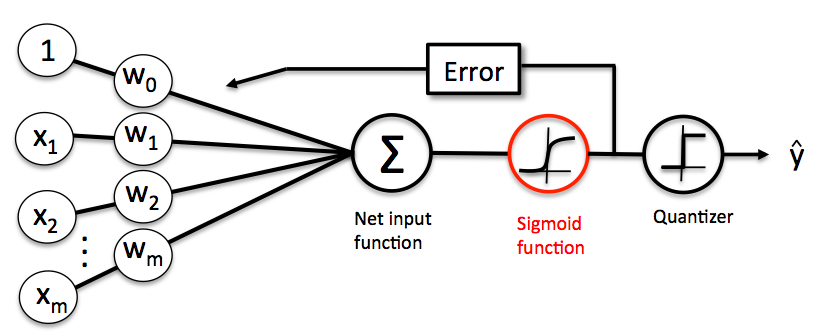
lr = LogisticRegression(C = 1000.0, random_state = 0, solver = "liblinear", multi_class = "ovr")
lr.fit(X_train_std, y_train)
y_pred = lr.predict(X_test_std)
# plot decision regions
fig, ax = plt.subplots(figsize=(8,6))
X_combined_std = np.vstack((X_train_std, X_test_std))
y_combined = np.hstack((y_train, y_test))
plot_decision_regions(X_combined_std, y_combined,
classifier=lr, test_idx=range(y_train.size,
y_train.size + y_test.size))
plt.xlabel('Petal length [Standardized]')
plt.ylabel('Petal width [Standardized]')
plt.legend(loc=4, prop={'size': 15})
plt.tight_layout()
for item in ([ax.title, ax.xaxis.label, ax.yaxis.label] +
ax.get_xticklabels() + ax.get_yticklabels()):
item.set_fontsize(20)
for item in (ax.get_xticklabels() + ax.get_yticklabels()):
item.set_fontsize(15)
plt.savefig('./output/fig-logistic-regression-boundray-3.png', dpi=300)
plt.show()
# plot confusion matrix
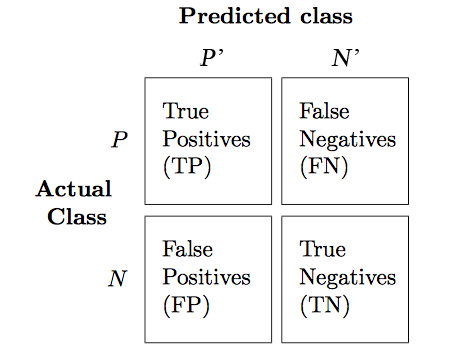
confmat = confusion_matrix(y_true=y_test, y_pred=y_pred)
fig, ax = plt.subplots(figsize=(5,5))
ax.matshow(confmat, cmap=plt.cm.Blues, alpha=0.3)
for i in range(confmat.shape[0]):
for j in range(confmat.shape[1]):
ax.text(x=j, y=i, s=confmat[i, j], va='center', ha='center')
plt.xlabel('Predicted label')
plt.ylabel('True label')
plt.tight_layout()
for item in ([ax.title, ax.xaxis.label, ax.yaxis.label] +
ax.get_xticklabels() + ax.get_yticklabels()):
item.set_fontsize(20)
for item in (ax.get_xticklabels() + ax.get_yticklabels()):
item.set_fontsize(15)
plt.savefig('./output/fig-logistic-regression-confusion-3.png', dpi=300)
plt.show()
# metrics
print('[Precision]')
p = precision_score(y_true=y_test, y_pred=y_pred, average=None)
print('Individual: %.2f, %.2f, %.2f' % (p[0], p[1], p[2]))
p = precision_score(y_true=y_test, y_pred=y_pred, average='micro')
print('Micro: %.2f' % p)
p = precision_score(y_true=y_test, y_pred=y_pred, average='macro')
print('Macro: %.2f' % p)
print('\n[Recall]')
r = recall_score(y_true=y_test, y_pred=y_pred,average=None)
print('Individual: %.2f, %.2f, %.2f' % (r[0], r[1], r[2]))
r = recall_score(y_true=y_test, y_pred=y_pred, average='micro')
print('Micro: %.2f' % r)
r = recall_score(y_true=y_test, y_pred=y_pred, average='macro')
print('Macro: %.2f' % r)
print('\n[F1-score]')
f = f1_score(y_true=y_test, y_pred=y_pred, average=None)
print('Individual: %.2f, %.2f, %.2f' % (f[0], f[1], f[2]))
f = f1_score(y_true=y_test, y_pred=y_pred, average='micro')
print('Micro: %.2f' % f)
f = f1_score(y_true=y_test, y_pred=y_pred, average='macro')
print('Macro: %.2f' % f)