Word2Vec

Shan-Hung Wu & DataLab Fall 2026

Neural Language Model

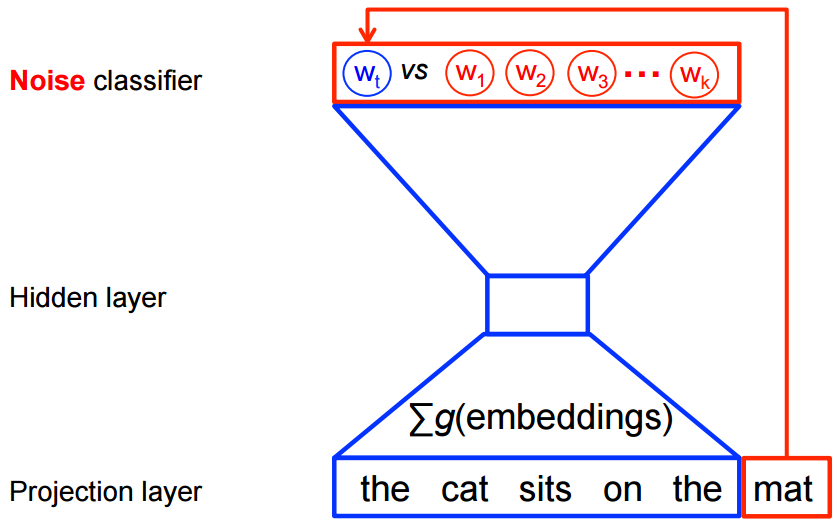
Neural probabilistic language models are traditionally trained using the maximum likelihood principle to estimate the probability distribution of the next word $w_t \in Vocabulary$ ($t$ for "targets") given the previous words $h$ ($h$ for "history") in terms of a softmax function. In other words, we build a multi-label classification model whose classes include all the words in the vocabulary.

Scenario of traditional laguage model task:

Note that the network outputs the entire distribution for all words in the vocabulary set, not only the most likely word (the red "here" in the image).

The classic neural language model (Bengio et al., 2001; 2003) contains three layers:

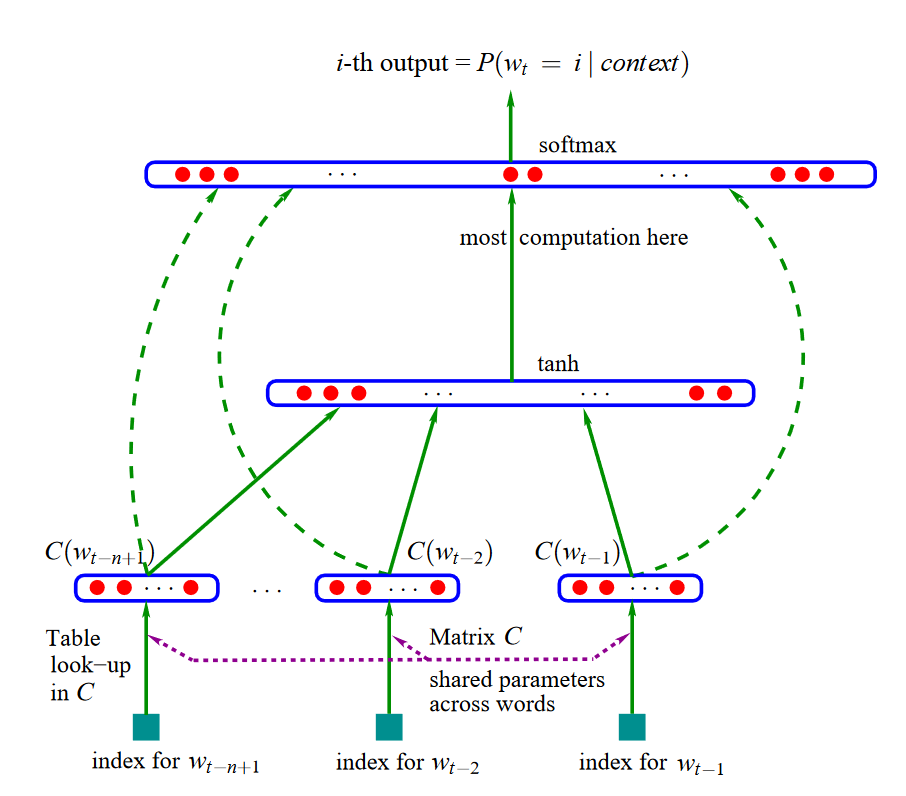
• Embedding Layer: a layer that generates word embeddings by multiplying an index vector with a word embedding matrix.The layer can be understood as a lookup table that maps from integer indices (which stand for specific words) to dense vectors (their embeddings);
• Intermediate Layer(s): one or more layers that concatenate inputs and produce an intermediate representation, e.g. a fully-connected layer that applies a non-linearity to the concatenation of word embeddings of n previous words;
• Softmax Layer: the final layer that produces a probability distribution over words in $V$.

The probability distribution of the next words $w_t \in Vocab$

$$P(w_t|h)=\textrm{softmax}(\textrm{score}(w_t,h))=\frac{\textrm{exp}\{\textrm{score}(w_t,h)\}}{\sum_{\textrm{Word w in Vocab}}\textrm{exp}\{\textrm{score}(w,h)\}}$$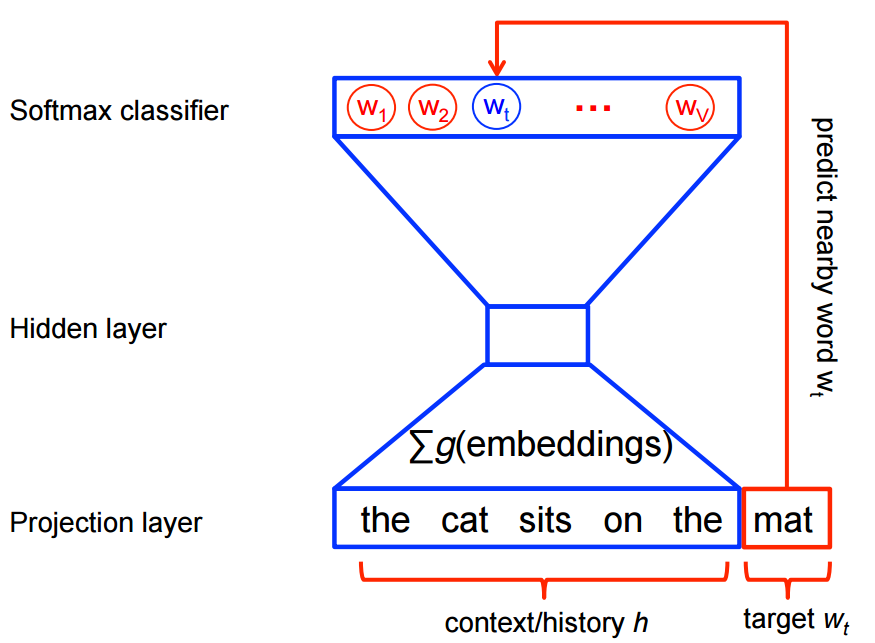

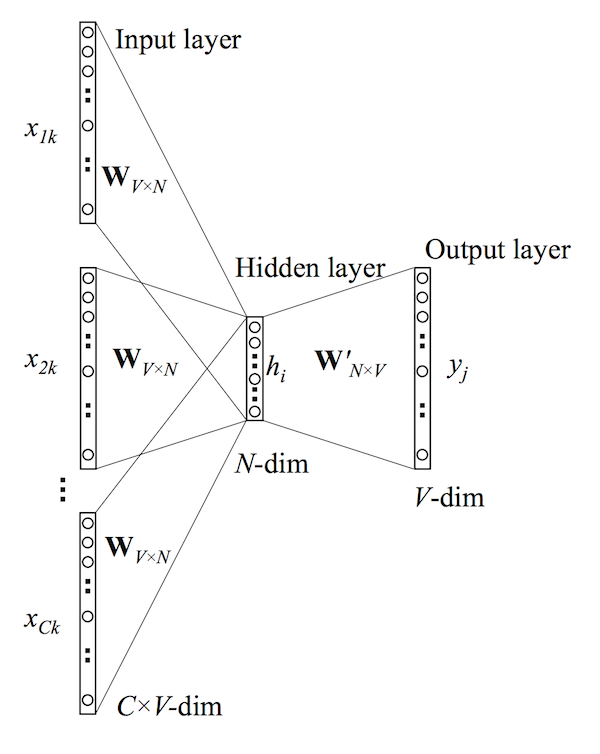
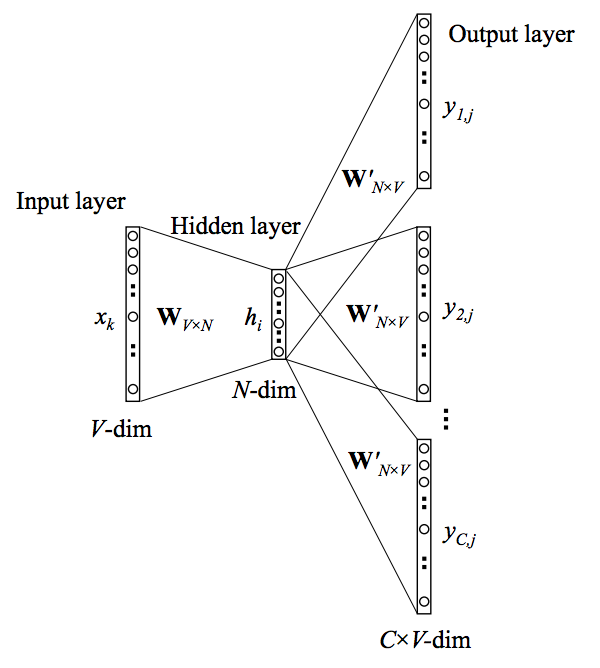
where $\textrm{score}(w_t,h)$ computes the compatibility of words $w_t$ with the context $h$. We train this model by maximizing its log-likelihood on the training set, i.e. by maximizing $$ \log(P(w_t|h))=\textrm{score}(w_t,h)-\log\Bigg(\sum_{\textrm{Word w in Vocab}}\textrm{exp}\{\textrm{score}(w,h)\}\Bigg) $$

This yields a properly normalized probabilistic model for language modeling. However, this is computationally expensive since the cost of computing "softmax" is proportional to the number of words in vocabulary which is typically on the order of hundreds of thousands or millions. We will need the softmax operation to normalize probability distribution at every training step.

Word2Vec

Reference:

• Vector Representations of Words

Neural language model is only able to look at the past words for its predictions, as it is evaluated on its ability to predict each next word in the corpus. However, a model that just aims to generate accurate word embeddings does not suffer from this restriction. Word2Vec is a computationally-efficient model that learns to embed words into vectors accurately. The goal is to map words that have similar meanings close to each other.

Why represent words as vectors?

When we dealing with words, a straightforward way would be treating each word as discrete symbols. For instance, cat as 2 and dog as 1. However, these symbols carry no information about the relationships, making it impossible for us to infer the relationship between cats and dogs (both are four-legged animals and pets) based on the 1 and 2 alone. Hence, to successfully learn the relationship between them, we need a better representation.
Vector space models (VSMs) which represent words as vectors can help overcome these obstacles. This is based on a key observation that semantically similar words are often interchangeable. For example, the words cat and dog may both appear in a context "___ is my favorite pet." When feeding cat and dog into the embedding networks, these two words will be likely to share the same/similar hidden representations.

Skip-Gram and CBOW

There are two variants of word2vec methods: Skip-Gram and CBOW (Continuous Bag-Of-Words). Algorithmically, these models are similar. CBOW predicts the target words using its neighborhood(context) whereas Skip-Gram does the inverse, which predicts context words from the target words. For example, given the sentence the quick brown fox jumped over the lazy dog. Defining the context words as the word to the left and right of the target word, CBOW will be trained on the dataset:

([the, brown], quick), ([quick, fox], brown), ([brown, jumped], fox)...

where CBOW tries to predict the target word quick from the context words in brackets [the, brown], and predict brown from [quick, fox] and so on. However, with Skip-Gram, the dataset becomes

(quick, the), (quick, brown), (brown, quick), (brown, fox), ...

where Skip-Gram predicts the context word the, brown with the target word quick. Statistically, CBOW smoothes over a lot of the distributional information (by treating an entire context as one example). For the most part, this turns out to be a useful thing for smaller datasets. On the other hand, Skip-Gram treats each context-target pair as a new observation and is shown to be able to capture the semantics better when we have a large dataset.

CBOW	Skip-gram

Note that the tasks described above are only used to train the embedding network, we don’t use the whole neural network. What we want is the weights of the hidden layer, the "embedding matrix".

For the rest of the tutorial, we will focus on the Skip-Gram model.

A Solution for the Softmax: Approximation with Noise Contrastive Estimation

Let's recap the objective which is to maximize log-likelihood: $$ \underset{\theta}{\textrm{argmax}} \ \textrm{score}(w_t,h)-\log\Bigg[\sum_{\textrm{w} \in \textrm{Vocab}}\textrm{exp}\ (\textrm{score}(w,h))\Bigg] $$ Mathematically, the gradient of the objective function is

$$ \nabla_{\theta} \ \textrm{score}(w_t,h) - \mathop{\mathbb{E}}_{\tilde{w} \sim P_{noise}}[\nabla_{\theta} \ \textrm{score}(\tilde{w},h)] $$ The gradient essentially has two parts: a positive reinforcement for the target word $w_t$ (the first term in the above equation) and a negative reinforcement for all other words $\tilde{w}$, which is weighted by their probability (the second term). In practice, since we don't want to sum over the probabilities for all words in the vocabulary, we approximate the expectation term of the negative reinforcement by drawing noise words and pairing with the target word $w_t$ to form the negative samples. Then, the expectation of these negative smaples can be an approximation of the real expectation.

With the skip-gram word2vec, we do not need a full probabilistic model. Since we have positive samples from the corpus and negative samples obtained from random sampling, the models instead can be trained with logistic regression objective to discriminate the target words $w_t$ from $k$ noise words $\tilde{w}$ (random samples, or unigram samples), given the same context. It designates all correct words $w_t$ given their context $c_i$ in the context window as true (y=1) and all noise samples $\tilde{w}$ as false (y=0). We illustrate this below for a CBOW model. For skip-gram, simply switch words "mat" and "the cat sit on the" in the box.

The objective of skip-gram with noise contrastive estimation(NCE) is to maximize:

$$ \log Q_\theta(D=1|w_t,h)+k\mathop{\mathbb{E}}_{\tilde{w} \sim P_{noise}}[\log Q_\theta(D=0|\tilde{w},h)] $$

where $Q$ is the simplfied distribution (often, unigram distribution), $Q_\theta(D=1|w_t,h)$ is the probability of that word $w_t$ existing in the context window $h$ appears in the dataset $D$ (probability of the positive pair $(w_t, h)$ appears in the corpus). And $Q_\theta(D=0|\tilde{w},h)$ is the probability of that word $\tilde{w}$ existing in the context window $h$ don't exist in the dataset $D$ (probability of the negative pair $(\tilde{w}, h)$ is not in the corpus). PyTorch does not provide a high level API of NCE loss, so we implement it ourselves and demonstrate the skip-gram algorithm with it in the following sections. In practice, $Q_\theta(D=1|w,h)$ is computed from the score and the noise distribution as

$$ Q_\theta(D=1|w,h)=\frac{\textrm{exp}\{\textrm{score}(w,h)\}}{\textrm{exp}\{\textrm{score}(w,h)\}+k\,P_{noise}(w)}=\sigma\big(\textrm{score}(w,h)-\log(k\,P_{noise}(w))\big) $$

where $\sigma$ is the sigmoid function and $Q_\theta(D=0|w,h)=1-Q_\theta(D=1|w,h)$. Note that no sum over the vocabulary is needed.

For students intersted in the deduction of the formula, here are the reference, reference2, and detail implementation.

Skip-gram with NCE Loss in PyTorch

The Dataset

The dataset we use is text8, which is the first 100 MB of cleaned text of the English Wikipedia dump on Mar. 3, 2006. While 100MB is not enough to train really good embeddings, we can still see some interesting relations. Splitting the text by blank space, we can find that there are 17,005,207 tokens in total.

Preparing training data

To generate batches for training, several functions defined below are used. First, we read the data into the memory and build the vocabulary using a number of most commonly seen words. Meanwhile, we build two dictionaries, a dictionary that translates words to indices and another which does the reverse. Then, for every word in the text selected as the center word, pair them with one of the context words. Finally, a python generator which generates a batch of pairs of center-target pairs.

import torch
import torch.nn as nn
import torch.nn.functional as F
import numpy as np
import random

device = torch.device('cuda' if torch.cuda.is_available() else
                      'mps' if torch.backends.mps.is_available() else 'cpu')
print('Using device:', device)

Using device: mps

import os
import urllib.request

# Download the data.
DOWNLOAD_URL = 'http://mattmahoney.net/dc/'
DATA_FOLDER = "data"
FILE_NAME = "text8.zip"
EXPECTED_BYTES = 31344016

def make_dir(path):
    """ Create a directory if there isn't one already. """
    try:
        os.mkdir(path)
    except OSError:
        pass
    
def download(file_name, expected_bytes):
    """ Download the dataset text8 if it's not already downloaded """
    local_file_path = os.path.join(DATA_FOLDER, file_name)
    if os.path.exists(local_file_path):
        print("Dataset ready")
        return local_file_path
    file_name, _ = urllib.request.urlretrieve(os.path.join(DOWNLOAD_URL, file_name), local_file_path)
    file_stat = os.stat(local_file_path)
    if file_stat.st_size == expected_bytes:
        print('Successfully downloaded the file', file_name)
    else:
        raise Exception(
              'File ' + file_name +
              ' might be corrupted. You should try downloading it with a browser.')
    return local_file_path    
    
make_dir(DATA_FOLDER)
file_path = download(FILE_NAME, EXPECTED_BYTES)

Dataset ready

import zipfile

# Read the data into a list of strings.
def read_data(file_path):
    """ Read data into a list of tokens """
    with zipfile.ZipFile(file_path) as f:
        # decode bytes into string
        data = f.read(f.namelist()[0]).decode('utf-8').split()
    return data

vocabulary = read_data(file_path)
print('Data size', len(vocabulary))

Data size 17005207

vocabulary[:5]

['anarchism', 'originated', 'as', 'a', 'term']

Build the dictionary

In CBOW and skip-gram, negative reinforcement can be approximated with non-context word pairs.

import collections
# Build the dictionary and replace rare words with UNK token.
def build_dataset(words, n_words):
    """ Create two dictionaries and count of occuring words
        - word_to_id: map of words to their codes
        - id_to_word: maps codes to words (inverse word_to_id)
        - count: map of words to count of occurrences
    """
    # map unknown words to -1
    count = [['UNK', -1]]
    # count of occurences for words in vocabulary
    count.extend(collections.Counter(words).most_common(n_words - 1)) 
    word_to_id = dict() # (word, id)
    # record word id
    for word, _ in count:
        word_to_id[word] = len(word_to_id)
    id_to_word = dict(zip(word_to_id.values(), word_to_id.keys())) # (id, word)
    return word_to_id, id_to_word, count

def convert_words_to_id(words, dictionary, count):
    """ Replace each word in the dataset with its index in the dictionary """
    data_w2id = []
    unk_count = 0
    for word in words:
        # return 0 if word is not in dictionary
        index = dictionary.get(word, 0)
        if index == 0:
            unk_count += 1
        data_w2id.append(index)
    count[0][1] = unk_count
    return data_w2id, count

"""Filling 4 global variables:
# data_w2id - list of codes (integers from 0 to vocabulary_size-1).
              This is the original text but words are replaced by their codes
# count - map of words(strings) to count of occurrences
# word_to_id - map of words(strings) to their codes(integers)
# id_to_word - maps codes(integers) to words(strings)
"""

vocabulary_size = 50000
word_to_id, id_to_word, count = build_dataset(vocabulary, vocabulary_size)
data_w2id, count = convert_words_to_id(vocabulary, word_to_id, count)
del vocabulary  # reduce memory.

print('Most common words (+UNK)', count[:5])
print('Sample data: {}'.format(data_w2id[:10]))
print([id_to_word[i] for i in data_w2id[:10]])

Most common words (+UNK) [['UNK', 418391], ('the', 1061396), ('of', 593677), ('and', 416629), ('one', 411764)]
Sample data: [5234, 3081, 12, 6, 195, 2, 3134, 46, 59, 156]
['anarchism', 'originated', 'as', 'a', 'term', 'of', 'abuse', 'first', 'used', 'against']

# utility function
def generate_sample(center_words, context_window_size):
    """ Form training pairs according to the skip-gram model. """
    for idx, center in enumerate(center_words):
        context = random.randint(1, context_window_size)
        # get a random target before the center word
        for target in center_words[max(0, idx - context) : idx]:
            yield center, target
        # get a random target after the center word
        for target in center_words[idx + 1 : idx + context + 1]:
            yield center, target

def batch_generator(data, skip_window, batch_size):
    """ Group a numeric stream into batches and yield them as Numpy arrays. """
    single_gen = generate_sample(data, skip_window)
    while True:
        center_batch = np.zeros(batch_size, dtype=np.int32)
        target_batch = np.zeros([batch_size, 1], dtype=np.int32)
        for idx in range(batch_size):
            center_batch[idx], target_batch[idx] = next(single_gen)
        yield center_batch, target_batch

Skip-gram word2vec model

Reference:

• Build the Neural Network (torch.nn.Module)

## some training settings
training_steps = 80000
skip_step = 2000

## some hyperparameters
batch_size = 512
embed_size = 512
num_sampled = 256
learning_rate = 1.0

## noise distribution P_noise(w) for NCE: unigram distribution raised to the 3/4 power
word_count = np.array([c for _, c in count], dtype=np.float64)
noise_dist = word_count ** 0.75
noise_dist = torch.tensor(noise_dist / noise_dist.sum(), dtype=torch.float)

• Layer Subclassing

# embedding matrix - hidden layer
class embedding_lookup(nn.Module):
    def __init__(self):
        super(embedding_lookup, self).__init__()
        self.embedding_matrix = nn.Parameter(torch.empty(vocabulary_size, embed_size))
        nn.init.xavier_uniform_(self.embedding_matrix)   # Glorot uniform

    def forward(self, inputs):
        center_words = inputs
        embedding = F.embedding(center_words, self.embedding_matrix)
        return embedding

    def extra_repr(self):
        return 'embedding_matrix: {}'.format(list(self.embedding_matrix.shape))

# context matrix - prediction layer
class nce_loss(nn.Module):
    def __init__(self):
        super(nce_loss, self).__init__()
        self.nce_weight = nn.Parameter(torch.empty(vocabulary_size, embed_size))
        nn.init.trunc_normal_(self.nce_weight, std=1.0/(embed_size ** 0.5))
        self.nce_bias = nn.Parameter(torch.zeros(vocabulary_size))
        self.register_buffer('noise_dist', noise_dist)   # P_noise(w)

    def forward(self, inputs):
        embedding, target_words = inputs[0], inputs[1]
        # sample k distinct noise words, shared by the whole batch (as tf.nn.nce_loss does)
        noise_words = torch.multinomial(self.noise_dist, num_sampled, replacement=False)
        # score(w, h) = h . w + b
        true_score = (embedding * self.nce_weight[target_words]).sum(1) + self.nce_bias[target_words]   # [batch_size]
        noise_score = embedding @ self.nce_weight[noise_words].T + self.nce_bias[noise_words]           # [batch_size, k]
        # Q(D=1|w,h) = sigmoid(score - log(expected count of w in the k noise words))
        # with k distinct noise words the expected count is 1 - exp(-k * P_noise(w)):
        # about k * P_noise(w) for rare words, but never larger than 1 for frequent words
        true_logits = true_score - torch.log(-torch.expm1(-num_sampled * self.noise_dist[target_words]))
        noise_logits = noise_score - torch.log(-torch.expm1(-num_sampled * self.noise_dist[noise_words]))
        # target words are labeled 1 (D=1), noise words are labeled 0 (D=0)
        true_loss = F.binary_cross_entropy_with_logits(true_logits, torch.ones_like(true_logits), reduction='none')
        noise_loss = F.binary_cross_entropy_with_logits(noise_logits, torch.zeros_like(noise_logits), reduction='none').sum(1)
        loss = torch.mean(true_loss + noise_loss)
        return loss

    def extra_repr(self):
        return 'nce_weight: {}, nce_bias: {}'.format(list(self.nce_weight.shape), list(self.nce_bias.shape))

• Model as a Function

embedding_layer = embedding_lookup().to(device)
nce_layer = nce_loss().to(device)

def word2vec(center_words, target_words):
    embedding = embedding_layer(center_words)
    loss = nce_layer((embedding, target_words))
    return loss

word2vec_parameters = list(embedding_layer.parameters()) + list(nce_layer.parameters())

print(embedding_layer)
print(nce_layer)
print('Total params:', sum(p.numel() for p in word2vec_parameters))

embedding_lookup(embedding_matrix: [50000, 512])
nce_loss(nce_weight: [50000, 512], nce_bias: [50000])
Total params: 51250000

## python generator that yields batches of (center_words, target_words)
batch_gen = batch_generator(data_w2id, 2, batch_size)

train_loss = []
optimizer = torch.optim.SGD(word2vec_parameters, lr=learning_rate, momentum=0.1, nesterov=True)

def train_step(center_words, target_words):
    loss = word2vec(center_words, target_words)
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    train_loss.append(loss.item())

x = []
y = []
for step, (center_words, target_words) in enumerate(batch_gen):
    if step == training_steps:
        break
    center_words = torch.from_numpy(center_words).long().to(device)
    target_words = torch.from_numpy(target_words).long().squeeze(1).to(device)
    train_step(center_words, target_words)

    if ((step+1) % skip_step) == 0:
        template = 'Step {:0}, Loss: {:.2f}'
        x.append(step+1)
        y.append(np.mean(train_loss))
        print(template.format(step+1, y[-1]))
        train_loss = []

Step 2000, Loss: 180.12
Step 4000, Loss: 31.39
Step 6000, Loss: 16.16
Step 8000, Loss: 11.10
Step 10000, Loss: 10.01
Step 12000, Loss: 8.99
Step 14000, Loss: 8.32
Step 16000, Loss: 7.56
Step 18000, Loss: 7.26
Step 20000, Loss: 7.02
Step 22000, Loss: 6.98
Step 24000, Loss: 6.73
Step 26000, Loss: 6.61
Step 28000, Loss: 6.42
Step 30000, Loss: 6.48
Step 32000, Loss: 6.41
Step 34000, Loss: 6.25
Step 36000, Loss: 6.27
Step 38000, Loss: 6.16
Step 40000, Loss: 6.11
Step 42000, Loss: 6.10
Step 44000, Loss: 5.91
Step 46000, Loss: 5.89
Step 48000, Loss: 5.96
Step 50000, Loss: 5.84
Step 52000, Loss: 5.85
Step 54000, Loss: 5.98
Step 56000, Loss: 5.85
Step 58000, Loss: 5.80
Step 60000, Loss: 5.88
Step 62000, Loss: 5.77
Step 64000, Loss: 5.76
Step 66000, Loss: 5.85
Step 68000, Loss: 5.75
Step 70000, Loss: 5.69
Step 72000, Loss: 5.80
Step 74000, Loss: 5.71
Step 76000, Loss: 5.41
Step 78000, Loss: 5.55
Step 80000, Loss: 5.64

%matplotlib inline
import matplotlib.pyplot as plt

plt.xlabel("steps")
plt.ylabel("loss")
plt.title("Learning Curve")
plt.plot(x, y)
plt.show()

Visualizing the learned embeddings

After training we can visualize the learned embeddings using t-SNE.
We can see that similar words are near to each other.

# get embedding matrix from model weights. > embedding_layer.embedding_matrix
embedding_matrix = embedding_layer.embedding_matrix.detach().cpu()

def plot_with_labels(low_dim_embs, labels):
    assert low_dim_embs.shape[0] >= len(labels), 'More labels than embeddings'
    plt.figure(figsize=(18, 18), dpi=150)  # in inches
    for i, label in enumerate(labels):
        x, y = low_dim_embs[i, :]
        plt.scatter(x, y)
        plt.annotate(
            label,
            xy=(x, y),
            xytext=(5, 2),
            textcoords='offset points',
            ha='right',
            va='bottom')

from sklearn.manifold import TSNE

tsne = TSNE(perplexity=30, n_components=2, init='pca', max_iter=5000, method='exact', learning_rate='auto')
plot_only = 400
final_embeddings = embedding_matrix
low_dim_embs = tsne.fit_transform(final_embeddings[:plot_only, :])
labels = [id_to_word[i] for i in range(plot_only)]
plot_with_labels(low_dim_embs, labels)

Cosine Similarity

cosine similarity is a simple metrics for evaluating the similarity between two vectors. $$ \newcommand{\norm}[1]{\left\lVert#1\right\rVert} \textrm{similarity} = \cos(\theta) = \frac{\textrm{A} \cdot \textrm{B}}{\norm{\textrm{A}} \cdot \norm{\textrm{B}}} $$

import numpy.linalg as LA

# handy method for calculating the similarity between 2 word
def cos_sim(word1, word2):
    id1 = word_to_id[word1]
    id2 = word_to_id[word2]
    
    vec1 = embedding_matrix[id1].numpy()
    vec2 = embedding_matrix[id2].numpy()

    return np.dot(vec1, vec2) / (LA.norm(vec1) * LA.norm(vec2))

cos_sim('cat', 'dog'), cos_sim('man', 'woman')

(np.float32(0.9811026), np.float32(0.9197146))

def top_k_nearest(word, k):
    vec = embedding_matrix[word_to_id[word]].numpy()
    
    # calaulate cosine similarity  of `vec` and all other vocabularies
    dot = np.dot(embedding_matrix.numpy(), vec)
    embedding_norm = LA.norm(embedding_matrix.numpy(), axis=-1)
    vec_norm = LA.norm(vec)
    norm_product = embedding_norm * vec_norm
    cos_sim = dot / norm_product
    
    # print out top k nearest words
    indices = np.argsort(cos_sim)[::-1][:k]
    print('---top {} nearest words of {}---'.format(k, word))
    for idx in indices:
        print(id_to_word[idx])
    print('\n')

top_k_nearest('england', 5)
top_k_nearest('rock', 5)

---top 5 nearest words of england---
england
spain
italy
mexico
france


---top 5 nearest words of rock---
rock
jazz
pop
folk
dance

Assignment

1. Devise Word2Vec model by subclassing torch.nn.Module

import torch.nn as nn

class Word2Vec(nn.Module):
    def __init__(self):
        super().__init__()
        '''To-Do: Define model variables'''

    def forward(self, center_words, target_words):
        '''To-Do: Define data flow and return loss'''

2. Train your word2vec model and plot your learning curve
   • Your learning curve should look similar to the example above.
3. Visualize your embedding matrix by t-SNE
4. Show top-5 nearest neighbors of two words.(pick by yourself)
5. Submit your ipynb to eeclass with the format Lab10_{student_id}.ipynb.

• Deadline: 2026-10-21 (Wed) 23:59