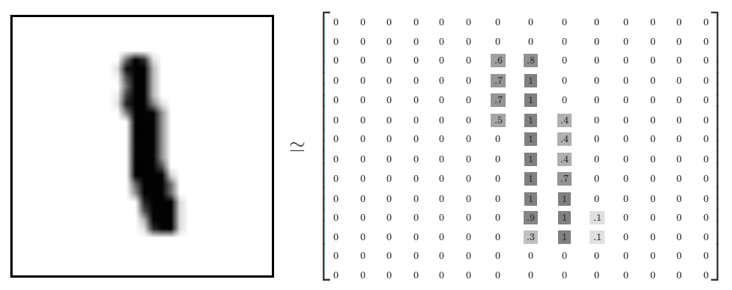
(<tf.Tensor: shape=(3, 1), dtype=string, numpy=
array([[b'Open'],
[b'Read'],
[b'Map']], dtype=object)>, <tf.Tensor: shape=(3, 2), dtype=float32, numpy=
array([[4.9066819e+05, 2.9742192e-03],
[4.9066819e+05, 2.3807518e-06],
[4.9066838e+05, 4.5068976e-02]], dtype=float32)>, <tf.Tensor: shape=(3, 3), dtype=int32, numpy=
array([[ 1, 0, -1],
[ 1, 0, 0],
[ 1, 0, 0]], dtype=int32)>, <tf.Tensor: shape=(24, 24, 3), dtype=float32, numpy=
array([[[ 0.794585 , 0.1525154 , -0.43435538],
[ 0.794585 , 0.20373973, -0.36603695],
[ 0.48714247, -0.08662798, -0.6393299 ],
...,
[ 0.94831586, 0.40871426, -0.1098188 ],
[ 0.8458286 , 0.2891522 , -0.21230607],
[ 0.77751017, 0.27207744, -0.19521199]],
[[ 0.40173 , -0.35992092, -1.1005033 ],
[ 0.23092432, -0.49657702, -1.2029905 ],
[ 0.06011866, -0.65028864, -1.3225526 ],
...,
[ 0.35048637, -0.34284613, -1.0151101 ],
[ 0.28216797, -0.42823932, -1.1005033 ],
[ 0.33341157, -0.35992092, -0.98094124]],
[[ 0.17968069, -0.53072655, -1.2200654 ],
[ 0.16260591, -0.5136518 , -1.2029905 ],
[ 0.16260591, -0.49657702, -1.1688217 ],
...,
[ 0.26509318, -0.41116452, -1.1005033 ],
[ 0.29924273, -0.41116452, -1.1005033 ],
[ 0.11136229, -0.599045 , -1.23714 ]],
...,
[[ 1.4607521 , 0.989469 , 0.5563291 ],
[ 1.3582649 , 0.818644 , 0.30011094],
[ 1.1703844 , 0.4428831 , -0.2635497 ],
...,
[ 0.45297363, 0.13542132, -1.2883837 ],
[ 0.60670453, 0.13542132, -1.1859157 ],
[ 1.3070213 , 0.92115057, -0.53684264]],
[[ 1.2387029 , 0.47703266, -0.17813721],
[ 1.204534 , 0.47703266, -0.12689358],
[ 1.477827 , 0.7332508 , 0.06098687],
...,
[ 0.17968069, 0.23790859, -1.7837453 ],
[ 0.77751017, 0.47703266, -1.2029905 ],
[ 1.6486326 , 1.2969115 , -0.21230607]],
[[ 1.1362156 , 0.22083381, -0.5710115 ],
[ 1.1020467 , 0.25498337, -0.46852422],
[ 1.3070213 , 0.56244516, -0.16106243],
...,
[-0.00819975, 0.0841777 , -1.80082 ],
[ 0.9653906 , 0.69908196, -0.87845397],
[ 1.4949018 , 1.1261058 , -0.2635497 ]]], dtype=float32)>, <tf.Tensor: shape=(10,), dtype=float32, numpy=array([0., 0., 0., 0., 0., 0., 1., 0., 0., 0.], dtype=float32)>)
now time 490668.42789291
-------------------------------------------------------------------------------
(<tf.Tensor: shape=(3, 1), dtype=string, numpy=
array([[b'Open'],
[b'Read'],
[b'Map']], dtype=object)>, <tf.Tensor: shape=(3, 2), dtype=float32, numpy=
array([[-1.0000000e+00, -1.0000000e+00],
[ 4.9066844e+05, 2.3807518e-06],
[ 4.9066847e+05, 1.1549212e-02]], dtype=float32)>, <tf.Tensor: shape=(3, 3), dtype=int32, numpy=
array([[ 1, 0, -1],
[ 1, 0, 1],
[ 1, 0, 1]], dtype=int32)>, <tf.Tensor: shape=(24, 24, 3), dtype=float32, numpy=
array([[[ 0.47468224, 0.75477153, 0.97282755],
[ 0.60898346, 0.90586287, 1.0399684 ],
[-0.0289228 , 0.1840257 , 0.06633849],
...,
[-1.1200638 , -1.1253278 , -1.3437556 ],
[-0.83467126, -0.82316476, -1.142294 ],
[-0.8850416 , -0.83995485, -1.3605261 ]],
[[ 0.5082624 , 0.72121096, 0.8049462 ],
[ 0.5754032 , 0.73800105, 0.73780537],
[-0.16320443, -0.10134721, -0.25261462],
...,
[-1.0025526 , -0.9910462 , -1.2765952 ],
[-0.86825144, -0.83995485, -1.2094544 ],
[-0.8011107 , -0.77281404, -1.2430346 ]],
[[ 0.44110203, 0.6540505 , 0.63708436],
[ 0.5754032 , 0.73800105, 0.67066455],
[ 0.45789215, 0.5197689 , 0.3852916 ],
...,
[-1.0193232 , -0.9910462 , -1.3773162 ],
[-0.9018317 , -0.8735351 , -1.2933853 ],
[-1.0864836 , -1.058187 , -1.4780372 ]],
...,
[[-1.3886466 , -1.461071 , -1.3101754 ],
[-1.4893676 , -1.4946316 , -1.4612471 ],
[-0.33108583, -0.11813731, -0.2694047 ],
...,
[ 1.1629392 , 0.8722827 , -0.05117261],
[ 1.1293786 , 0.82193196, -0.10152333],
[ 1.146149 , 0.7883518 , -0.16868371]],
[[-1.3718565 , -1.4442809 , -1.2933853 ],
[-1.3550664 , -1.37714 , -1.3773162 ],
[-0.41501674, -0.28599912, -0.48761725],
...,
[ 0.35717112, 0.1000948 , -0.58833826],
[ 0.5082624 , 0.2679566 , -0.45405665],
[ 0.7600551 , 0.45260853, -0.3701257 ]],
[[-1.7915306 , -1.847165 , -1.74662 ],
[-1.7915306 , -1.8303748 , -1.7802002 ],
[-1.5732985 , -1.561792 , -1.5955483 ],
...,
[-1.5229282 , -1.7967947 , -2.0823634 ],
[-1.4725775 , -1.6793032 , -1.9648522 ],
[-1.2543454 , -1.4946316 , -1.8809212 ]]], dtype=float32)>, <tf.Tensor: shape=(10,), dtype=float32, numpy=array([0., 0., 0., 0., 0., 0., 0., 0., 0., 1.], dtype=float32)>)
now time 490668.499416673
-------------------------------------------------------------------------------