In this lab, we will introduce the conception of Markov Decision Process(MDP) and two solution algorithms, and then we will introduce the Q-Learning and SARSA algorithm, finally we will use the Q-learning algorithm to train an agent to play "Flappy Bird" game.
Markov Decision Process(MDP)¶
A Markov decision process (MDP) is a random process, i.e. a sequence of random states S1, S2, ... with the Markov property. It provides a mathematical framework for modeling decision making in situations where outcomes are partly random and partly under the control of a decision maker.
There are two algorithms to solve the MDP problem: value iteration and policy iteration.
Value iteration¶
The algorithm is like below:
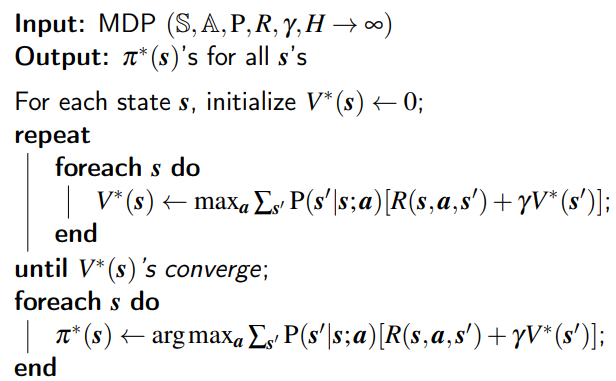
Next, we will show an example code of Gridworld to see how value iteration works.
please install gym.
commands: pip install gym==0.21.0
(If you cannot install the package successfully, please check your pip and pip setuptools version. You can refer to this)
import numpy as np
import sys
from gym.envs.toy_text import discrete
# four actions in the game
UP = 0
RIGHT = 1
DOWN = 2
LEFT = 3
class GridworldEnv(discrete.DiscreteEnv):
"""
Grid World environment from Sutton's Reinforcement Learning book chapter 4.
You are an agent on an MxN grid and your goal is to reach the terminal
state at the top left or the bottom right corner.
For example, a 4x4 grid looks as follows:
T o o o
o x o o
o o o o
o o o T
x is your position and T are the two terminal states.
You can take actions in each direction (UP=0, RIGHT=1, DOWN=2, LEFT=3).
Actions going off the edge leave you in your current state.
You receive a reward of -1 at each step until you reach a terminal state.
"""
metadata = {'render.modes': ['human', 'ansi']}
def __init__(self, shape=[4, 4]):
if not isinstance(shape, (list, tuple)) or not len(shape) == 2:
raise ValueError('shape argument must be a list/tuple of length 2')
self.shape = shape
nS = np.prod(shape)
nA = 4
MAX_Y = shape[0]
MAX_X = shape[1]
P = {}
grid = np.arange(nS).reshape(shape)
it = np.nditer(grid, flags=['multi_index'])
while not it.finished:
s = it.iterindex
y, x = it.multi_index
P[s] = {a: [] for a in range(nA)}
is_done = lambda s: s == 0 or s == (nS - 1)
reward = 0.0 if is_done(s) else -1.0
# We're stuck in a terminal state
if is_done(s):
P[s][UP] = [(1.0, s, reward, True)]
P[s][RIGHT] = [(1.0, s, reward, True)]
P[s][DOWN] = [(1.0, s, reward, True)]
P[s][LEFT] = [(1.0, s, reward, True)]
# Not a terminal state
else:
ns_up = s if y == 0 else s - MAX_X
ns_right = s if x == (MAX_X - 1) else s + 1
ns_down = s if y == (MAX_Y - 1) else s + MAX_X
ns_left = s if x == 0 else s - 1
P[s][UP] = [(1.0, ns_up, reward, is_done(ns_up))]
P[s][RIGHT] = [(1.0, ns_right, reward, is_done(ns_right))]
P[s][DOWN] = [(1.0, ns_down, reward, is_done(ns_down))]
P[s][LEFT] = [(1.0, ns_left, reward, is_done(ns_left))]
it.iternext()
# Initial state distribution is uniform
isd = np.ones(nS) / nS
# We expose the model of the environment for educational purposes
# This should not be used in any model-free learning algorithm
self.P = P
super(GridworldEnv, self).__init__(nS, nA, P, isd)
def render(self, mode='human', close=False):
if close:
return
outfile = StringIO() if mode == 'ansi' else sys.stdout
grid = np.arange(self.nS).reshape(self.shape)
it = np.nditer(grid, flags=['multi_index'])
while not it.finished:
s = it.iterindex
y, x = it.multi_index
if self.s == s:
output = " x "
elif s == 0 or s == self.nS - 1:
output = " T "
else:
output = " o "
if x == 0:
output = output.lstrip()
if x == self.shape[1] - 1:
output = output.rstrip()
outfile.write(output)
if x == self.shape[1] - 1:
outfile.write("\n")
it.iternext()
env = GridworldEnv()
def value_iteration(env, theta=0.0001, discount_factor=1.0):
"""
Value Iteration Algorithm.
Args:
env: OpenAI env. env.P represents the transition probabilities of the environment.
env.P[s][a] is a list of transition tuples (prob, next_state, reward, done).
env.nS is a number of states in the environment.
env.nA is a number of actions in the environment.
theta: We stop evaluation once our value function change is less than theta for all states.
discount_factor: Gamma discount factor.
Returns:
A tuple (policy, V) of the optimal policy and the optimal value function.
"""
def one_step_lookahead(state, V):
"""
Given an state, calculate the new value function V(s) based on the value iteration algorithm
Args:
state: represents each state in the Gridworld, an integer
V: the current value function of the states(V(s)), the lengh is env.nS
Returns:
a new V(s)
"""
A = np.zeros(env.nA)
for a in range(env.nA):
for prob, next_state, reward, done in env.P[state][a]:
A[a] += prob * (reward + discount_factor * V[next_state])
return A
V = np.zeros(env.nS)
while True:
delta = 0
for s in range(env.nS):
# Do a one-step lookahead to find the best action
A = one_step_lookahead(s, V)
best_action_value = np.max(A)
# Calculate delta across all states seen so far
delta = max(delta, np.abs(best_action_value - V[s]))
# Update the value function
V[s] = best_action_value
# Check if we can stop
if delta < theta:
break
# Create a deterministic policy using the optimal value function
policy = np.zeros([env.nS, env.nA])
for s in range(env.nS):
# One step lookahead to find the best action for this state
A = one_step_lookahead(s, V)
best_action = np.argmax(A)
# Always take the best action
policy[s, best_action] = 1.0
return policy, V
policy, v = value_iteration(env)
print("Policy Probability Distribution:")
print(policy)
print("")
print("Reshaped Grid Policy (0=up, 1=right, 2=down, 3=left):")
print(np.reshape(np.argmax(policy, axis=1), env.shape))
print("")
print("Value Function:")
print(v)
print("")
print("Reshaped Grid Value Function:")
print(v.reshape(env.shape))
print("")
Policy Probability Distribution: [[1. 0. 0. 0.] [0. 0. 0. 1.] [0. 0. 0. 1.] [0. 0. 1. 0.] [1. 0. 0. 0.] [1. 0. 0. 0.] [1. 0. 0. 0.] [0. 0. 1. 0.] [1. 0. 0. 0.] [1. 0. 0. 0.] [0. 1. 0. 0.] [0. 0. 1. 0.] [1. 0. 0. 0.] [0. 1. 0. 0.] [0. 1. 0. 0.] [1. 0. 0. 0.]] Reshaped Grid Policy (0=up, 1=right, 2=down, 3=left): [[0 3 3 2] [0 0 0 2] [0 0 1 2] [0 1 1 0]] Value Function: [ 0. -1. -2. -3. -1. -2. -3. -2. -2. -3. -2. -1. -3. -2. -1. 0.] Reshaped Grid Value Function: [[ 0. -1. -2. -3.] [-1. -2. -3. -2.] [-2. -3. -2. -1.] [-3. -2. -1. 0.]]
Policy iteration¶
The algorithm is like below:

Next, we will show an example code of Gridworld to see how value iteration works.
import numpy as np
import sys
from gym.envs.toy_text import discrete
env = GridworldEnv()
def policy_eval(policy, env, discount_factor=1.0, theta=0.00001):
"""
Evaluate a policy given an environment and a full description of the environment's dynamics.
Args:
policy: [S, A] shaped matrix representing the policy.
env: OpenAI env. env.P represents the transition probabilities of the environment.
env.P[s][a] is a list of transition tuples (prob, next_state, reward, done).
env.nS is a number of states in the environment.
env.nA is a number of actions in the environment.
theta: We stop evaluation once our value function change is less than theta for all states.
discount_factor: Gamma discount factor.
Returns:
Vector of length env.nS representing the value function.
"""
# Start with a random (all 0) value function
V = np.zeros(env.nS)
while True:
delta = 0
# For each state, perform a "full backup"
for s in range(env.nS):
v = 0
# Look at the possible next actions
for a, action_prob in enumerate(policy[s]):
# For each action, look at the possible next states...
for prob, next_state, reward, done in env.P[s][a]:
# Calculate the expected value
v += action_prob * prob * (reward + discount_factor * V[next_state])
# How much our value function changed (across any states)
delta = max(delta, np.abs(v - V[s]))
V[s] = v
# Stop evaluating once our value function change is below a threshold
if delta < theta:
break
return np.array(V)
def policy_improvement(env, policy_eval_fn=policy_eval, discount_factor=1.0):
"""
Policy Improvement Algorithm. Iteratively evaluates and improves a policy
until an optimal policy is found.
Args:
env: The OpenAI environment.
policy_eval_fn: Policy Evaluation function that takes 3 arguments:
policy, env, discount_factor.
discount_factor: gamma discount factor.
Returns:
A tuple (policy, V).
policy is the optimal policy, a matrix of shape [S, A] where each state s
contains a valid probability distribution over actions.
V is the value function for the optimal policy.
"""
def one_step_lookahead(state, V):
"""
Helper function to calculate the value for all action in a given state.
Args:
state: The state to consider (int)
V: The value to use as an estimator, Vector of length env.nS
Returns:
A vector of length env.nA containing the expected value of each action.
"""
A = np.zeros(env.nA)
for a in range(env.nA):
for prob, next_state, reward, done in env.P[state][a]:
A[a] += prob * (reward + discount_factor * V[next_state])
return A
# Start with a random policy
policy = np.ones([env.nS, env.nA]) / env.nA
while True:
# Evaluate the current policy
V = policy_eval_fn(policy, env, discount_factor)
# Will be set to false if we make any changes to the policy
policy_stable = True
# For each state...
for s in range(env.nS):
# The best action we would take under the current policy
chosen_a = np.argmax(policy[s])
# Find the best action by one-step lookahead
# Ties are resolved arbitarily
action_values = one_step_lookahead(s, V)
best_a = np.argmax(action_values)
# Greedily update the policy
if chosen_a != best_a:
policy_stable = False
policy[s] = np.eye(env.nA)[best_a]
# If the policy is stable we've found an optimal policy. Return it
if policy_stable:
return policy, V
policy, v = policy_improvement(env)
print("Policy Probability Distribution:")
print(policy)
print("")
print("Reshaped Grid Policy (0=up, 1=right, 2=down, 3=left):")
print(np.reshape(np.argmax(policy, axis=1), env.shape))
print("")
print("Value Function:")
print(v)
print("")
print("Reshaped Grid Value Function:")
print(v.reshape(env.shape))
print("")
Policy Probability Distribution: [[1. 0. 0. 0.] [0. 0. 0. 1.] [0. 0. 0. 1.] [0. 0. 1. 0.] [1. 0. 0. 0.] [1. 0. 0. 0.] [1. 0. 0. 0.] [0. 0. 1. 0.] [1. 0. 0. 0.] [1. 0. 0. 0.] [0. 1. 0. 0.] [0. 0. 1. 0.] [1. 0. 0. 0.] [0. 1. 0. 0.] [0. 1. 0. 0.] [1. 0. 0. 0.]] Reshaped Grid Policy (0=up, 1=right, 2=down, 3=left): [[0 3 3 2] [0 0 0 2] [0 0 1 2] [0 1 1 0]] Value Function: [ 0. -1. -2. -3. -1. -2. -3. -2. -2. -3. -2. -1. -3. -2. -1. 0.] Reshaped Grid Value Function: [[ 0. -1. -2. -3.] [-1. -2. -3. -2.] [-2. -3. -2. -1.] [-3. -2. -1. 0.]]
Value iteration VS. Policy iteration¶
Difference:¶

Q-Learning¶
Q-Learning is an off-policy, model-free RL algorithm.

SARSA¶
SARSA is an on-policy, model-free RL algorithm.

Q-Learning VS. SARSA¶
Difference:¶

Flappy Bird Game¶
Flappybird is a side-scrolling game where the agent must successfully nagivate through gaps between pipes.
Next, we wiil train an agent to play "Flappy Bird" game using Q-learning algorithm.

First, we should install PyGame Learning Environment(PLE) which provides the environment to train an agent.
1. Clone the repo¶
command:
git clone https://github.com/ntasfi/PyGame-Learning-Environment

2. Install PLE (in the PyGame-Learning-Environment folder)¶
command:
cd PyGame-Learning-Environment
pip install -e .
3. Install pygame (1.9.6)¶
command: pip install pygame
Now, we can train our agent to play the game.
It is not necessary to create the code file in the in the PyGame-Learning-Environment folder, you could create the code file wherever you want.
Code¶
from ple.games.flappybird import FlappyBird
from ple import PLE
import matplotlib.pyplot as plt
import os
import numpy as np
%matplotlib inline
os.environ["SDL_VIDEODRIVER"] = "dummy" # this line disable pop-out window
game = FlappyBird()
env = PLE(game, fps=30, display_screen=False) # environment interface to game
env.reset_game()
pygame 2.5.2 (SDL 2.28.3, Python 3.9.18) Hello from the pygame community. https://www.pygame.org/contribute.html couldn't import doomish Couldn't import doom
# return a dictionary whose key is action description and value is action index
print(game.actions)
# return a list of action index (include None)
print(env.getActionSet())
{'up': 119}
[119, None]
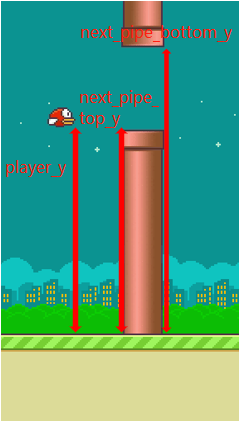
# a dictionary describe state
'''
player y position.
players velocity.
next pipe distance to player
next pipe top y position
next pipe bottom y position
next next pipe distance to player
next next pipe top y position
next next pipe bottom y position
'''
game.getGameState()
{'player_y': 256,
'player_vel': 0,
'next_pipe_dist_to_player': 309.0,
'next_pipe_top_y': 144,
'next_pipe_bottom_y': 244,
'next_next_pipe_dist_to_player': 453.0,
'next_next_pipe_top_y': 160,
'next_next_pipe_bottom_y': 260}
import math
import copy
from collections import defaultdict
MIN_EXPLORING_RATE = 0.01
MIN_LEARNING_RATE = 0.5
class Agent:
def __init__(self,
bucket_range_per_feature,
num_action,
t=0,
discount_factor=0.99):
self.update_parameters(t) # init explore rate and learning rate
self.q_table = defaultdict(lambda: np.zeros(num_action))
self.discount_factor = discount_factor
self.num_action = num_action
# how to discretize each feature in a state
# the higher each value, less time to train but with worser performance
# e.g. if range = 2, feature with value 1 is equal to feature with value 0 bacause int(1/2) = int(0/2)
self.bucket_range_per_feature = bucket_range_per_feature
def select_action(self, state):
# epsilon-greedy
state_idx = self.get_state_idx(state)
if np.random.rand() < self.exploring_rate:
action = np.random.choice(num_action) # Select a random action
else:
action = np.argmax(
self.q_table[state_idx]) # Select the action with the highest q
return action
def update_policy(self, state, action, reward, state_prime):
state_idx = self.get_state_idx(state)
state_prime_idx = self.get_state_idx(state_prime)
# Update Q_value using Q-learning update rule
best_q = np.max(self.q_table[state_prime_idx])
self.q_table[state_idx][action] += self.learning_rate * (
reward + self.discount_factor * best_q - self.q_table[state_idx][action])
def get_state_idx(self, state):
# instead of using absolute position of pipe, use relative position
state = copy.deepcopy(state)
state['next_next_pipe_bottom_y'] -= state['player_y']
state['next_next_pipe_top_y'] -= state['player_y']
state['next_pipe_bottom_y'] -= state['player_y']
state['next_pipe_top_y'] -= state['player_y']
# sort to make list converted from dict ordered in alphabet order
state_key = [k for k, v in sorted(state.items())]
# do bucketing to decrease state space to speed up training
state_idx = []
for key in state_key:
state_idx.append(
int(state[key] / self.bucket_range_per_feature[key]))
return tuple(state_idx)
def update_parameters(self, episode):
self.exploring_rate = max(MIN_EXPLORING_RATE,
min(0.5, 0.99**((episode) / 30)))
self.learning_rate = max(MIN_LEARNING_RATE, min(0.5, 0.99
** ((episode) / 30)))
def shutdown_explore(self):
# make action selection greedy
self.exploring_rate = 0
num_action = len(env.getActionSet())
bucket_range_per_feature = {
'next_next_pipe_bottom_y': 40,
'next_next_pipe_dist_to_player': 512,
'next_next_pipe_top_y': 40,
'next_pipe_bottom_y': 20,
'next_pipe_dist_to_player': 20,
'next_pipe_top_y': 20,
'player_vel': 4,
'player_y': 16
}
# init agent
agent = Agent(bucket_range_per_feature, num_action)
import moviepy.editor as mpy
def make_anim(images, fps=60, true_image=False):
duration = len(images) / fps
def make_frame(t):
try:
x = images[int(len(images) / duration * t)]
except:
x = images[-1]
if true_image:
return x.astype(np.uint8)
else:
return ((x + 1) / 2 * 255).astype(np.uint8)
clip = mpy.VideoClip(make_frame, duration=duration)
clip.fps = fps
return clip
from IPython.display import Image, display
reward_per_epoch = []
lifetime_per_epoch = []
exploring_rates = []
learning_rates = []
print_every_episode = 500
show_gif_every_episode = 5000
NUM_EPISODE = 40000
for episode in range(0, NUM_EPISODE):
# Reset the environment
env.reset_game()
# record frame
frames = [env.getScreenRGB()]
# for every 500 episodes, shutdown exploration to see performance of greedy action
if episode % print_every_episode == 0:
agent.shutdown_explore()
# the initial state
state = game.getGameState()
# cumulate reward for this episode
cum_reward = 0
t = 0
while not env.game_over():
# select an action
action = agent.select_action(state)
# execute the action and get reward
# reward = +1 when pass a pipe, -5 when die
reward = env.act(env.getActionSet()[action])
frames.append(env.getScreenRGB())
# cumulate reward
cum_reward += reward
# observe the result
state_prime = game.getGameState() # get next state
# update agent
agent.update_policy(state, action, reward, state_prime)
# Setting up for the next iteration
state = state_prime
t += 1
# update exploring_rate and learning_rate
agent.update_parameters(episode)
if episode % print_every_episode == 0:
print("Episode {} finished after {} time steps, cumulated reward: {}, exploring rate: {}, learning rate: {}".format(
episode,
t,
cum_reward,
agent.exploring_rate,
agent.learning_rate
))
reward_per_epoch.append(cum_reward)
exploring_rates.append(agent.exploring_rate)
learning_rates.append(agent.learning_rate)
lifetime_per_epoch.append(t)
# for every 5000 episode, record an animation
if episode % show_gif_every_episode == 0:
print("len frames:", len(frames))
clip = make_anim(frames, fps=60, true_image=True).rotate(-90)
display(clip.ipython_display(fps=60, autoplay=1, loop=1))
Episode 0 finished after 62 time steps, cumulated reward: -5.0, exploring rate: 0.5, learning rate: 0.5 len frames: 63 Moviepy - Building video __temp__.mp4. Moviepy - Writing video __temp__.mp4
Moviepy - Done ! Moviepy - video ready __temp__.mp4
Episode 500 finished after 62 time steps, cumulated reward: -5.0, exploring rate: 0.5, learning rate: 0.5 Episode 1000 finished after 62 time steps, cumulated reward: -5.0, exploring rate: 0.5, learning rate: 0.5 Episode 1500 finished after 62 time steps, cumulated reward: -5.0, exploring rate: 0.5, learning rate: 0.5 Episode 2000 finished after 62 time steps, cumulated reward: -5.0, exploring rate: 0.5, learning rate: 0.5 Episode 2500 finished after 62 time steps, cumulated reward: -5.0, exploring rate: 0.43277903725889943, learning rate: 0.5 Episode 3000 finished after 62 time steps, cumulated reward: -5.0, exploring rate: 0.3660323412732292, learning rate: 0.5 Episode 3500 finished after 62 time steps, cumulated reward: -5.0, exploring rate: 0.30957986252419073, learning rate: 0.5 Episode 4000 finished after 65 time steps, cumulated reward: -5.0, exploring rate: 0.26183394327157605, learning rate: 0.5 Episode 4500 finished after 62 time steps, cumulated reward: -5.0, exploring rate: 0.22145178723886091, learning rate: 0.5 Episode 5000 finished after 62 time steps, cumulated reward: -5.0, exploring rate: 0.18729769509073985, learning rate: 0.5 len frames: 63 Moviepy - Building video __temp__.mp4. Moviepy - Writing video __temp__.mp4
Moviepy - Done ! Moviepy - video ready __temp__.mp4
Episode 5500 finished after 62 time steps, cumulated reward: -5.0, exploring rate: 0.15841112426184903, learning rate: 0.5 Episode 6000 finished after 62 time steps, cumulated reward: -5.0, exploring rate: 0.13397967485796172, learning rate: 0.5 Episode 6500 finished after 59 time steps, cumulated reward: -5.0, exploring rate: 0.11331624189077398, learning rate: 0.5 Episode 7000 finished after 62 time steps, cumulated reward: -5.0, exploring rate: 0.09583969128049684, learning rate: 0.5 Episode 7500 finished after 62 time steps, cumulated reward: -5.0, exploring rate: 0.08105851616218128, learning rate: 0.5 Episode 8000 finished after 62 time steps, cumulated reward: -5.0, exploring rate: 0.0685570138491429, learning rate: 0.5 Episode 8500 finished after 62 time steps, cumulated reward: -5.0, exploring rate: 0.05798359469728905, learning rate: 0.5 Episode 9000 finished after 62 time steps, cumulated reward: -5.0, exploring rate: 0.04904089407128572, learning rate: 0.5 Episode 9500 finished after 98 time steps, cumulated reward: -4.0, exploring rate: 0.04147740932356356, learning rate: 0.5 Episode 10000 finished after 83 time steps, cumulated reward: -4.0, exploring rate: 0.03508042658630376, learning rate: 0.5 len frames: 84 Moviepy - Building video __temp__.mp4. Moviepy - Writing video __temp__.mp4
Moviepy - Done ! Moviepy - video ready __temp__.mp4
Episode 10500 finished after 54 time steps, cumulated reward: -5.0, exploring rate: 0.029670038450977102, learning rate: 0.5 Episode 11000 finished after 106 time steps, cumulated reward: -3.0, exploring rate: 0.02509408428990297, learning rate: 0.5 Episode 11500 finished after 175 time steps, cumulated reward: -2.0, exploring rate: 0.021223870922486707, learning rate: 0.5 Episode 12000 finished after 62 time steps, cumulated reward: -5.0, exploring rate: 0.017950553275045137, learning rate: 0.5 Episode 12500 finished after 62 time steps, cumulated reward: -5.0, exploring rate: 0.015182073244652034, learning rate: 0.5 Episode 13000 finished after 66 time steps, cumulated reward: -4.0, exploring rate: 0.012840570676248398, learning rate: 0.5 Episode 13500 finished after 62 time steps, cumulated reward: -5.0, exploring rate: 0.010860193639877882, learning rate: 0.5 Episode 14000 finished after 140 time steps, cumulated reward: -2.0, exploring rate: 0.01, learning rate: 0.5 Episode 14500 finished after 134 time steps, cumulated reward: -3.0, exploring rate: 0.01, learning rate: 0.5 Episode 15000 finished after 100 time steps, cumulated reward: -4.0, exploring rate: 0.01, learning rate: 0.5 len frames: 101 Moviepy - Building video __temp__.mp4. Moviepy - Writing video __temp__.mp4
Moviepy - Done ! Moviepy - video ready __temp__.mp4
Episode 15500 finished after 98 time steps, cumulated reward: -4.0, exploring rate: 0.01, learning rate: 0.5 Episode 16000 finished after 62 time steps, cumulated reward: -5.0, exploring rate: 0.01, learning rate: 0.5 Episode 16500 finished after 175 time steps, cumulated reward: -2.0, exploring rate: 0.01, learning rate: 0.5 Episode 17000 finished after 61 time steps, cumulated reward: -5.0, exploring rate: 0.01, learning rate: 0.5 Episode 17500 finished after 67 time steps, cumulated reward: -4.0, exploring rate: 0.01, learning rate: 0.5 Episode 18000 finished after 71 time steps, cumulated reward: -4.0, exploring rate: 0.01, learning rate: 0.5 Episode 18500 finished after 514 time steps, cumulated reward: 7.0, exploring rate: 0.01, learning rate: 0.5 Episode 19000 finished after 337 time steps, cumulated reward: 3.0, exploring rate: 0.01, learning rate: 0.5 Episode 19500 finished after 360 time steps, cumulated reward: 3.0, exploring rate: 0.01, learning rate: 0.5 Episode 20000 finished after 98 time steps, cumulated reward: -4.0, exploring rate: 0.01, learning rate: 0.5 len frames: 99 Moviepy - Building video __temp__.mp4. Moviepy - Writing video __temp__.mp4
Moviepy - Done ! Moviepy - video ready __temp__.mp4
Episode 20500 finished after 473 time steps, cumulated reward: 6.0, exploring rate: 0.01, learning rate: 0.5 Episode 21000 finished after 98 time steps, cumulated reward: -4.0, exploring rate: 0.01, learning rate: 0.5 Episode 21500 finished after 134 time steps, cumulated reward: -3.0, exploring rate: 0.01, learning rate: 0.5 Episode 22000 finished after 866 time steps, cumulated reward: 17.0, exploring rate: 0.01, learning rate: 0.5 Episode 22500 finished after 206 time steps, cumulated reward: -1.0, exploring rate: 0.01, learning rate: 0.5 Episode 23000 finished after 225 time steps, cumulated reward: 0.0, exploring rate: 0.01, learning rate: 0.5 Episode 23500 finished after 145 time steps, cumulated reward: -2.0, exploring rate: 0.01, learning rate: 0.5 Episode 24000 finished after 360 time steps, cumulated reward: 3.0, exploring rate: 0.01, learning rate: 0.5 Episode 24500 finished after 247 time steps, cumulated reward: 0.0, exploring rate: 0.01, learning rate: 0.5 Episode 25000 finished after 62 time steps, cumulated reward: -5.0, exploring rate: 0.01, learning rate: 0.5 len frames: 63 Moviepy - Building video __temp__.mp4. Moviepy - Writing video __temp__.mp4
Moviepy - Done ! Moviepy - video ready __temp__.mp4
Episode 25500 finished after 329 time steps, cumulated reward: 3.0, exploring rate: 0.01, learning rate: 0.5 Episode 26000 finished after 134 time steps, cumulated reward: -3.0, exploring rate: 0.01, learning rate: 0.5 Episode 26500 finished after 1012 time steps, cumulated reward: 21.0, exploring rate: 0.01, learning rate: 0.5 Episode 27000 finished after 627 time steps, cumulated reward: 10.0, exploring rate: 0.01, learning rate: 0.5 Episode 27500 finished after 175 time steps, cumulated reward: -2.0, exploring rate: 0.01, learning rate: 0.5 Episode 28000 finished after 247 time steps, cumulated reward: 0.0, exploring rate: 0.01, learning rate: 0.5 Episode 28500 finished after 1680 time steps, cumulated reward: 38.0, exploring rate: 0.01, learning rate: 0.5 Episode 29000 finished after 905 time steps, cumulated reward: 18.0, exploring rate: 0.01, learning rate: 0.5 Episode 29500 finished after 1079 time steps, cumulated reward: 22.0, exploring rate: 0.01, learning rate: 0.5 Episode 30000 finished after 1440 time steps, cumulated reward: 32.0, exploring rate: 0.01, learning rate: 0.5 len frames: 1441 Moviepy - Building video __temp__.mp4. Moviepy - Writing video __temp__.mp4
Moviepy - Done ! Moviepy - video ready __temp__.mp4
Episode 30500 finished after 1079 time steps, cumulated reward: 22.0, exploring rate: 0.01, learning rate: 0.5 Episode 31000 finished after 3072 time steps, cumulated reward: 75.0, exploring rate: 0.01, learning rate: 0.5 Episode 31500 finished after 1793 time steps, cumulated reward: 41.0, exploring rate: 0.01, learning rate: 0.5 Episode 32000 finished after 360 time steps, cumulated reward: 3.0, exploring rate: 0.01, learning rate: 0.5 Episode 32500 finished after 1418 time steps, cumulated reward: 31.0, exploring rate: 0.01, learning rate: 0.5 Episode 33000 finished after 2367 time steps, cumulated reward: 57.0, exploring rate: 0.01, learning rate: 0.5 Episode 33500 finished after 776 time steps, cumulated reward: 14.0, exploring rate: 0.01, learning rate: 0.5 Episode 34000 finished after 776 time steps, cumulated reward: 14.0, exploring rate: 0.01, learning rate: 0.5 Episode 34500 finished after 3724 time steps, cumulated reward: 93.0, exploring rate: 0.01, learning rate: 0.5 Episode 35000 finished after 3601 time steps, cumulated reward: 89.0, exploring rate: 0.01, learning rate: 0.5 len frames: 3602 Moviepy - Building video __temp__.mp4. Moviepy - Writing video __temp__.mp4
Moviepy - Done ! Moviepy - video ready __temp__.mp4
--------------------------------------------------------------------------- ValueError Traceback (most recent call last) Cell In[7], line 72 70 print("len frames:", len(frames)) 71 clip = make_anim(frames, fps=60, true_image=True).rotate(-90) ---> 72 display(clip.ipython_display(fps=60, autoplay=1, loop=1)) File c:\Users\ytwa\anaconda3\envs\tf2\lib\site-packages\moviepy\video\io\html_tools.py:220, in ipython_display(clip, filetype, maxduration, t, fps, rd_kwargs, center, **html_kwargs) 217 if t is not None: 218 clip = clip.to_ImageClip(t) --> 220 return HTML2(html_embed(clip, filetype=filetype, maxduration=maxduration, 221 center=center, rd_kwargs=rd_kwargs, **html_kwargs)) File c:\Users\ytwa\anaconda3\envs\tf2\lib\site-packages\moviepy\video\io\html_tools.py:107, in html_embed(clip, filetype, maxduration, rd_kwargs, center, **html_kwargs) 104 else: 105 raise ValueError("Unknown class for the clip. Cannot embed and preview.") --> 107 return html_embed(filename, maxduration=maxduration, rd_kwargs=rd_kwargs, 108 center=center, **html_kwargs) 110 filename = clip 111 options = " ".join(["%s='%s'"%(str(k), str(v)) for k,v in html_kwargs.items()]) File c:\Users\ytwa\anaconda3\envs\tf2\lib\site-packages\moviepy\video\io\html_tools.py:142, in html_embed(clip, filetype, maxduration, rd_kwargs, center, **html_kwargs) 140 duration = ffmpeg_parse_infos(filename)['duration'] 141 if duration > maxduration: --> 142 raise ValueError("The duration of video %s (%.1f) exceeds the 'maxduration' "%(filename, duration)+ 143 "attribute. You can increase 'maxduration', by passing 'maxduration' parameter" 144 "to ipython_display function." 145 "But note that embedding large videos may take all the memory away !") 147 with open(filename, "rb") as f: 148 data= b64encode(f.read()).decode("utf-8") ValueError: The duration of video __temp__.mp4 (60.0) exceeds the 'maxduration' attribute. You can increase 'maxduration', by passing 'maxduration' parameterto ipython_display function.But note that embedding large videos may take all the memory away !
def demo():
# Reset the environment
env.reset_game()
# record frame
frames = [env.getScreenRGB()]
# shutdown exploration to see performance of greedy action
agent.shutdown_explore()
# the initial state
state = game.getGameState()
while not env.game_over():
# select an action
action = agent.select_action(state)
# execute the action and get reward
reward = env.act(env.getActionSet()[action])
frames.append(env.getScreenRGB())
# observe the result
state_prime = game.getGameState() # get next state
# Setting up for the next iteration
state = state_prime
clip = make_anim(frames, fps=60, true_image=True).rotate(-90)
display(clip.ipython_display(fps=60, autoplay=1, loop=1))
demo()
Moviepy - Building video __temp__.mp4. Moviepy - Writing video __temp__.mp4
Moviepy - Done ! Moviepy - video ready __temp__.mp4
# plot life time against training episodes
fig, ax1 = plt.subplots(figsize=(20, 5))
plt.plot(range(len(lifetime_per_epoch)), lifetime_per_epoch)
fig.tight_layout()
plt.show()
# plot reward against training episodes
fig, ax1 = plt.subplots(figsize=(20, 5))
plt.plot(range(len(reward_per_epoch)), reward_per_epoch)
plt.show()
Reference Reading:¶
Assignment ¶
What you should do:¶
- Change the update rule from Q-learning to SARSA(with the same episodes).
- Give a brief report to discuss the result(compare Q-learning with SARSA based on the game result).
Requirements:¶
Implement SARSA (60%)
Write a brief report in the notebook, including the following sections:
- Plot the Lifetime per epoch (SARSA vs. Q-learning) (10%)
- Plot the Reward per epoch (SARSA vs. Q-learning) (10%)
- Discussion (Analyze and discuss the differences between Q-learning and SARSA based on the game results.) (10%)
Upload both
ipynbandmp4files to Google Drive- Lab14_{student_id}.ipynb (90%, just as the description above)
- Lab14_{student_id}.mp4 (10%, 1% per pipe)
Share your drive's link via eeclass
- Please make sure that TA can access your google drive!!!
- If the TA cannot access the file, you will receive a score of 0 for this lab.
Deadline: 2025-12-03(Wed) 23:59.